Piezopedia - Statisches Verhalten

Um eine Dehnung in einem piezoelektrischen Aktor zu erzeugen, muss die Piezokeramik vorpolarisiert sein. Die inneren Dipole sind damit mehrheitlich in eine Richtung orientiert.
Wird nun ein elektrisches Feld in Richtung der Dipole angelegt (hier z-Richtung), so dehnt sich der Aktor in Richtung des elektrischen Feldes aus (Längseffekt – longitudinaler Effekt) und zieht sich quer zum elektrischen Feld zusammen (Quereffekt – transversaler Effekt) (Abb. 4.1.).

Für den Aktor gilt folgende Zustandsgleichung:

longitudinaler Effekt

(4.0.1)

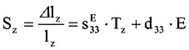
transversaler Effekt:

(4.0.2)

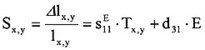
S – Belastung, T = F/A – mechanische Spannung (z.B. durch äußere Kräfte), s_ii – Elastizitätskoeffizient (Reziprok des Elastizitätsmoduls), Δl_z – Dehnung des Aktors in z-Richtung, l_z – Länge des piezoelektrisch aktiven Teils, L_o ist die Gesamtlänge der Keramik, c_F – Steifigkeit, Federkonstante einer äußeren Feder (z.B. Vorspannung); c_T – Steifigkeit des Translators

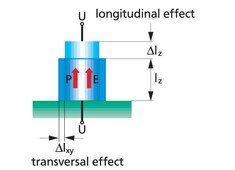
Abb. 4.1. longitudinaler und transversaler Effekt

Da die Fuß- und Endstücke oftmals Scheibendicke aufweisen, sind beide Längen in guter Näherung gleich.
Piezokeramiken, als gepolte ferroelektrische Keramiken, zeigen anisotrope Eigenschaften, die elastischen und die elektrischen Koeffizienten sind richtungsabhängig. Der erste Index in der d_ij Konstante zeigt die Richtung des angelegten elektrischen Feldes und der zweite ist die Richtung der induzierten Beanspruchung.

Für piezoelektrische Keramiken sind folgende Werte typisch:

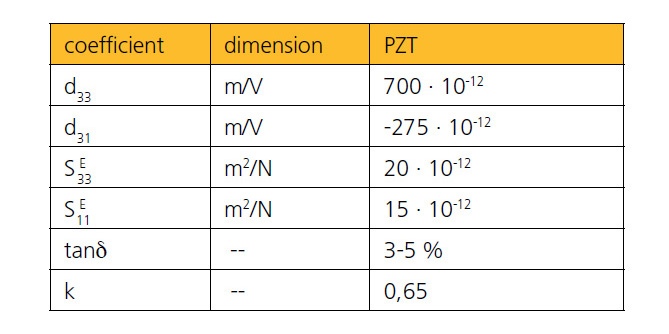
Das negative Vorzeichen der Ladungskonstante d31 verdeutlicht die Kontraktion als Ergebnis des Quereffektes. Im Allgemeinen bilden “Hard-PZT” Keramiken die Grundlage für Hochvoltaktoren und “Soft-PZT” die Grundlagen für Multilayer Niedervoltaktoren.

Wenn nicht ausdrücklich vermerkt, beziehen sich die weiteren Erläuterungen auf den Längseffekt. Alle weiteren Beziehungen können auch auf den transversalen Effekt angewendet werden.

(4.0.3)

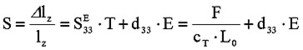
Der erste Term der Gleichung beschreibt die mechanischen Eigenschaften des Aktors, der in erster Näherung als Feder mit einer Federsteifigkeit c_T behandelt werden kann. Der zweite Term beschreibt die Ausdehnung in einem elektrischen Feld E. Das statische Verhalten eines Piezoaktors lässt sich anhand obiger Formel für einige Spezialfälle erläutern.

The actuator is short-circuited. Formula (4.0.3) becomes S = Δl/L₀ = s₃₃ · T. The deformation of the actuator Δl is determined by the stiffness of the actuator c_T^E because of the action of an external load with the pressure T, so it becomes “shorter“.

(4.1.1)

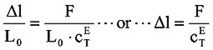
L₀ – Aktorhöhe c_T^E – Steifigkeit des Aktors

Für zusammengesetzte Aktoren (Piezostapel) berechnet sich die Steifigkeit aus der Steifigkeit der Einzelscheiben. Dieses gilt aber nur für Piezostapel mit ideal dünner Klebstoffschicht zwischen den Einzelscheiben. Monolithische Multilayer-Aktoren erfüllen diese Bedingung recht gut. Ihre Steifigkeiten liegen ca. 10 – 15 % unter denen der homogenen Keramik. Besonders bei Hochvoltstapeln mit metallischer Folie als Elektrode können die Eigenschaften des Elektrodenmaterials einen wesentlichen Einfluss auf die Gesamtsteifigkeit des Piezostapels haben.

Beispiel 13:

Auf einen Piezoaktor mit der Steifigkeit von c_T^E = 70N/µm wirkt eine äußere konstante Last von F=70N. Entsprechend Gleichung (4.1.1.) wird der Aktor um 1µm zusammengedrückt.

Es kommt ein unbelasteter Aktor (ohne Vorspannung) zur Anwendung. Auf diesen wirkt keine äußere Kraft F = 0:

(4.2.1)

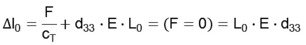
Die maximale Ausdehnung wird von der Stapellänge L₀ (genauer von der Länge des aktiven Materials), von dem verwendeten Keramikmaterial d₃₃ und von der angelegten Feldstärke E bestimmt.

Beispiel 14:

Betrachten wir einen Multilayer-Aktor mit folgenden Parametern:

Ladungskonstante d₃₃ = 635·10^-12m/V
aktive Länge L₀ = 16mm

Bei einer Einzelschichtdicke von 100µm wird eine Spannung von 150V angelegt: Feldstärke E = 1,5kV/mm

In Übereinstimmung mit Gleichung (4.2.1) beträgt die Ausdehnung ohne äußere Belastung Δl₀ = 15µm.

Auf das Piezoelement wirkt eine konstante äußere Kraft F (z.B. konstantes Gewicht). Das bedeutet, dass der Arbeitshub des Aktors lediglich um einen konstanten Betrag (siehe Bild 4.3.1.) verschoben wird (Nullpunkt-Verschiebung). Der Aktor wird zusammengedrückt..).

(4.3.1)

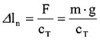
Die Längenänderung auf Grund des Piezoeffektes ist unverändert und erreicht den Wert des Leerlaufhubes (siehe Formel 4.2.1).

In einigen Fällen (materialabhängig) können bei genügend großen Kräften und im spannungslosen Zustand Depolarisationserscheinungen der Keramik eintreten.

Diese Depolarisationserscheinungen verschwinden aber nach dem Einschalten der Betriebsspannung. 

Eine weitere Erhöhung der Belastung führt zur irreversiblen Depolarisation und letztendlich zur mechanischen Beschädigung (Bruch der Keramikschichten und damit verbundene Spannungsdurchbrüche). Beachten Sie daher die aufbauabhängigen Belastungswerte der Materialien.

Standardaktoren von piezosystem jena mit einem Querschnitt von 5 x 5mm² zeigen Depolarisationseffekte bei externen Lasten > 1kN. Bitte beachten Sie die angegebenen Parameter in den spezifischen Produktdatenblättern.

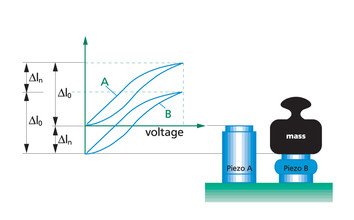
Abb. 4.3.1. relative Dehnung in Abhängigkeit einer konstanten Last

Betrachten wir als ein Beispiel einer veränderlichen Kraft die Wirkung einer äußeren Feder. Die auf das Piezoelement wirkende äußere Kraft F ist wegabhängig und nimmt mit der Ausdehnung des Aktors zu. Mit F = -c_F· ΔL (Element arbeitet gegen die Federsteifigkeit c_F) ergibt sich die Längenänderung zu:

(4.4.1)

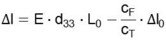
bzw. im Verhältnis zum Leerlaufhub:

(4.4.2)

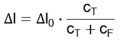
Ein Teil der durch den Piezoeffekt erzeugten Längenänderung wird durch die Elastizität des Elementes aufgebraucht (siehe Abb. 4.4.1.).

Sind die Steifigkeiten von Piezoaktor und äußerer Feder gleich, c_F = c_T, so erreicht der Piezoaktor nur noch die Hälfte seiner Nennausdehnung für eine bestimmte Spannung.

Beispiel 15:

Der Aktor PA 16/12 hat eine Steifigkeit von c_T = 65N/µm. Sein Leerlaufhub ?l₀ beträgt typ. 16µm. Dieser Aktor wird in ein Gehäuse mit einer Vorspannung c_F = 1/10 c_T eingebaut. In Übereinstimmung mit Gleichung (4.4.2.) verringert sich sein Hub auf 14,5µm. Wird die Vorspannung auf 70 % der Steifigkeit des Aktors erhöht c_F = 0,7 c_T = 46N/µm, so steht nur noch ein Hub von ?l = 9,4µm zur Verfügung (Abb. 4.3.2.).

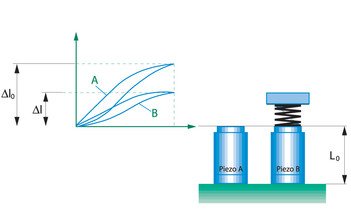
Abb 4.4.1. Änderung des Hubes bei einer Belastung (z.B. äußere Feder)

Aus Gleichung (4.4.2.) ergibt sich die effektive Kraft, die ein Piezotranslator in einer federnden Anordnung erzeugen kann zu:

(4.4.3)

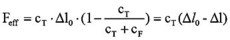
Δl₀ – Bewegung ohne externe Ladung (µm)
Δl – Bewegung mit externen Ladungen (µm)

Beispiel 16:

Es wird wieder ein Aktor PA 16/12 eingesetzt. Der Leerlaufhub beträgt Δl₀ = 16µm, die Steifigkeit C_T =65N/µm. Dieser Aktor arbeitet gegen eine Feder mit der Federsteifigkeit 64N/µm. In dieser Anordnung kann er eine effektive Kraft von ca. 516N erzeugen. Arbeitet er gegen eine äußere Feder mit einer Steifigkeit von 500N/µm, so kann er eine effektive Kraft von Feff = 920N aufbringen. Das sind 91% seiner Blockierkraft.

Für das vorliegende Beispiel bedeutet das eine Kraftentwicklung, die der Hälfte der maximalen vom Piezotranslator erzeugbaren Kraft entspricht (maximale Kraft s. auch Kapitel 4.5. Blockierkraft)

Eine äußere wegabhängige Kraft (z.B. Federkraft) auf den Aktor verringert seinen Hub und die zur Verfügung stehende Kraft.

In diesem Sinn stellt auch die Vorspannung eine äußere Kraft dar. Diese wird in der Regel in Größenordnung von 1/10 der Druckbelastung eingestellt. Damit ist die Wegverkürzung sehr gering. Dafür können Aktoren mit Vorspannung Zugkräfte aufnehmen und sind für dynamische Anwendungen geeignet! In jedem Fall ist um Schäden zu vermeiden zu beachten: max. Zugkraft < Vorspannungskraft

Der Piezoaktor ist zwischen zwei (unendlich steifen c_F) Wänden befestigt und kann sich nicht ausdehnen (siehe auch Gleichung 4.2.1.).

(4.5.1)

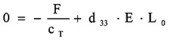
Der Piezoaktor entwickelt seine maximal erreichbare Kraft F_max.

(4.5.2)

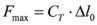
Diese Kraft wird auch Blockierkraft genannt.

Ein Piezotranslator, der gegen eine Federkraft arbeitet, zeigt folgende Abhängigkeit der generierten Kräfte von der erreichbaren Auslenkung. Das Belastungsdiagramm gilt für typische Aktoren von piezosystem jena.

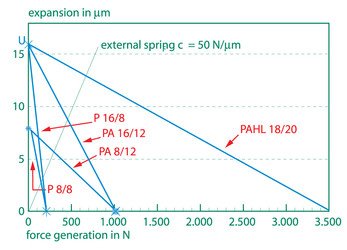
Abb. 4.5.1. Abhängigkeit der effektiven Kraft von der Auslenkung

Der Schnittpunkt mit der x-Achse kennzeichnet jeweils die Blockierkraft, der Schnittpunkt mit der y-Achse gibt an, welche maximale Wegverschiebung der Piezotranslator erzeugen kann. Der Schnittpunkt der eingezeichneten Federkennlinie einer äußeren Federkraft mit der jeweiligen Aktorkurve gibt die Parameter Δl; F_eff an, die in dieser Anordnung (Aktor arbeitet gegen diese Federkraft) erreicht werden.

Seine maximale mechanische Energie kann ein Piezotranslator umsetzen, wenn er gegen eine äußere Feder arbeitet, welche die Hälfte der Steifigkeit des Translators aufweist (c_F = ½·c_T). In diesem Fall erreicht der Piezotranslator nur 67% von seiner normalen Wegauslenkung.

Beispiel 17:

Ein Piezotranslator vom Typ PA 16/12 arbeitet gegen eine äußere Federkraft. Sein maximaler Hub unbelastet beträgt 16 µm. In der beschriebenen Anordnung soll er noch eine Kraft von 320 N aufbringen. Welchen Hub erreicht dieser Piezotranslator?

Antwort:

Entsprechend Bild 4.5.1. ist auf der x-Achse der Wert von 320N zu markieren. Der Schnittpunkt einer Senkrechten auf diesem Punkt mit der Kennlinie zeigt den noch erreichbaren Hub. Gleiches Ergebnis lässt sich auch durch Gleichung 4.4.3. (Kapitel 4.4. äußere Krafteinwirkung) bestimmen. Gleichung 4.4.3. umgestellt ergibt Δl = Δl₀ – F_eff /c_T. Mit dem entsprechenden Wert für die Steifigkeit des Aktors c_T = 85 N/µm erhält man Δl = 12,2 µm.

Bitte beachten Sie:

In der Realität können nicht unendlich steife Wände oder ein Spannen des Aktors realisiert werden; die Aktoren erreichen nicht ihre theoretisch mögliche maximale Kraft. Weiterhin zeigt der Aktor beim Blockieren keine Bewegung!

Begriffe & Erläuterungen

Fragen & Antworten