9. Messsysteme
Einführung
Der Einfluss der ferroelektrischen Hysterese und das zeitabhängigen Driftverhalten begrenzt die Positioniergenauigkeit piezoelektrischen Aktoren. Für viele Anwendungen spielen diese Effekte eine untergeordnete Rolle. Für andere Anwendungen ist es vorteilhaft, ein closed loop-System zu implementieren. In einem closed loop-System wird die Bewegung des Aktors gemessen und unerwünschte Abweichungen vom vorgegebenen Sollwert werder durch die Regelelektronik korrigiert.
piezosystem jena nutzt im wesentlichen zwei verschiedene Arten von Positionssensoren:
- DMS-Sensoren
- induktive Sensoren
- kapazitive Sensoren
Dehnmessstreifen (DMS) sind sehr kompakt. Sie können in fast alle piezoelektrischen Aktorsystemen von piezosystem jena integriert werden. Kapazitive Sensoren werden für Systeme benötigt, wo höchste Genauigkeit und / oder Dynamik im Vordergrund steht. Um die höchsten Messgenauigkeiten für spezielle Anforderungen zu erreichen, ist es erforderlich, die grundlegenden Eigenschaften der verschiedenen Sensorsysteme zu kennen. In allen Fällen muss berücksichtigt werden, dass für Genauigkeit im Bereich von Mikrometern und Nanometern das gesamte System optimiert werden muss (Aktor-, Sensor-, Elektronik-, Umgebungsbedingungen, etc.).
9.1 Auflösung
Der piezoelektrische Effekt ist ein echter Festkörper-Effekt. In der Theorie gibt es keine Beschränkung in der Auflösung; eine unendlich kleine Änderung im elektrischen Feld führt zu einer unendlich kleinen mechanischen Verschiebung. Die Realität setzt einige Grenzen in der Auflösung, die durch elektrisches, mechanisches, akustisches und thermisches Rauschen verursacht werden.
Mechanisch:
Die mechanische Auflösung wird durch die Auslegung des Antriebs bestimmt. Piezoaktoren von piezosysten jena sind mit Festkörpergelenken konstruiert. Durch dieses Konstruktionsprinzip entsteht grundsätzlich kein mechanisches Spiel, wodurch die mechanische Auflösung unbegrenzt ist.
Elektrisch:
Im Betrieb gibt die Auflösung an, welches die kleinste mögliche Schrittweite ist und wie weit sich der Piezoaktor bewegt wenn die Ausgangsspannung des Verstärkers konstant bleibt. Diese Auflösung wird durch das Rauschen der Ausgangsspannung der Steuerelektronik bestimmt. Wir betrachten hier nur den Frequenzbereich der Ausgangsspannung, welche auf den Aktor abgestimmt ist.
Übliche Piezosysteme mit integrierter Wegübersetzung von piezosystem jena verfügen über eine Resonanzfrequenz zwischen 200Hz und 750Hz, sodass die Ausgangsspannung nur bis zu dieser Frequenz gemessen wird. Frequenzen oberhalb dieses Bereichs können nicht in eine Bewegung durch einen Aktor umgewandelt werden. Eine Störspannung von 0,3mV begrenzt die mögliche Auflösung des Piezoaktor auf 0,2nm, bezogen auf ein Gesamtweg von z.B. 100µm @ 150V (gesamter Spannungsbereich: -20 … +130V).

Für die Auflösung im geschlossenen Regelkreis muss das Rauschen des Messsystems zusätzlich in Betracht gezogen werden. Daher wird das Rauschen der Ausgangsspannung im „closed loop“-Modus gemessen.
Dieser Wert hängt vom aktuell genutztem Aktor, dem Messsystem, den eingestellten Regelparametern und dem Verstärker ab. Die Berechnung der Auflösung erfolgt ebenfalls nach der oben genannten Formel.
Um die Auflösung eines closed loop-Systems zu bestimmen, verwendeten wir einen PX 100 mit integriertem kapazitiven Sensor und als Piezosteuereinheit ein NV 40/3 CLE. Die Untersuchungen wurden entsprechend den (oben erwähnten) bestmöglichen Umgebungsbedingungen durchgeführt. Das Piezoelement wurde mit einer Rechteckfunktion bei einer Amplitude von ungefähr 40mV Amplitude angesteuert.
In Abbildung 9.1.1. und 9.1.2. ist das Messsignal des Sensors und das entsprechende Messsignal eines Laserstrahl-Interferometers dargestellt.
Die Messungen wurden für zwei verschiedene Filter-Frequenzen der Sensorelektronik durchgeführt – Abbildung 9.1.1 mit 1kHz und Abbildung 9.1.2 mit 10Hz.
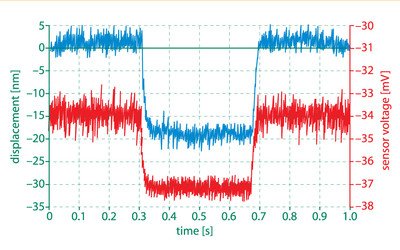
Abb. 9.1.1. Spannungssignal des kapazitiven Sensors (rote Linie) im Vergleich mit dem Interferrometersignal (blaue Linie). Die Filterfrequenz des Sensors wurde auf 1kHz eingestellt.
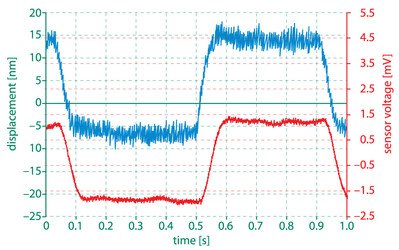
Abb. 9.1.2. Spannungssignal des kapazitiven Sensors (rote Linie) im Vergleich mit dem Interferrometersignal (blaue Linie). Die Filterfrequenz des Sensors wurde auf 10Hz eingestellt.
Man kann sehen, dass das Signal des kapazitiven Sensors bei einem 10Hz-Filter besseres Rauschverhalten hat als das Interferrometersignal. Der Grund dafür ist, dass höhere Frequenzen den 10Hz Filter der Elektronik nicht passieren und damit nicht gemessen werden. Es scheint, dass der Sensor ein geringeres Rauschen aufweist, was zu einer höheren Genauigkeit des gesamten Systems führen kann.
Bitte beachten Sie: Die höchste Positionierauflösung erfordert sehr stabile Messbedingungen. Die besten Messbedingungen sind:
- fester Unterbau (Fundament, Arbeitstisch/Granitplatte, feste Fixierung)
- keine elektromagnetischen Felder (geschirmte Kabel verwenden)
- Isolierung aller Schwingungen (eine aktiv gedämpfter Tisch wird empfohlen)
- stabile Temperaturverhältnisse
Ansonsten bestimmen die Umgebungsbedingungen die Auflösung des Experiments.
9.2. Linearität
Im Idealfall sollte das Verhältnis zwischen dem Eingangssignal (positionsgebendes Signal eines Aktors) und dem Ausgangssignal (realisiert Bewegung) linear sein. Wenn man über Systeme mit integrierten Sensoren spricht, ist die Linearität des Sensors (plus Sensorelektronik) ein wichtiges Qualitätsmerkmal.
Berechnung der absoluten Position durch die Empfindlichkeit
Die Linearität beschreibt die Annäherung des Verhältnisses zwischen angezeigter und wahrer Position. Mit der gemessenen Spannung (MON) wird, auf der Grundlage der untenstehenden Formel, die erreichte Position berechnet. Die aktuellen Werte für die folgenden Berechnungen sind dem Kalibrier-Protokoll aus Punkt 9.5 entnommen.

Beispiel 21:
minimale Spannung = – 0,007V*
Gesamthub = 400µm*s
Empfindlichkeit = 0,0248V/µm*
gemessene Spannung = 3,864V

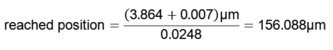
*Werte sind dem Messprotokoll entnommen
Absolute Position berechnet aus der Empfindlichkeit unter Berücksichtigung der Nichtlinearität
Wie bereits erwähnt, liefert die Monitorausgangsspannung den genauen Wert für die aktuelle Position des Systems. Die Abweichung der wahren Aktorposition von dieser linearen Beziehung ist die Nichtlinearität. Diese wird durch eine Polynomfunktion höherer Ordnung beschrieben. Um die wahre Aktorposition auf der Grundlage der gemessenen Spannung zu berechnen, muss die Nichtlinearität berücksichtigt werden.
Unter Berücksichtigung der gemessenen Nichtlinearität des Positioniersystems (siehe Kalibrierungskurve) sollte die absolute Position (aus der Empfindlichkeit berechnet) und mittels der Nichtlinearität korrigiert werden.

Beispiel 22:
minimale Spannung = – 0,007V*
Gesamthub = 400µm*
Empfindlichkeit = 0,0248V/µm*
Nichtlinearität @157µm = 0,037%
gemessene Spannung = 3.864V

= 156,088µm + 148nm
= 156,236µm
* Werte sind dem Messprotokoll entnommen
Unter Beachtung der Nichtlinearität von 148nm an der Position des Aktors von 156µm (MON = 3,864V) wurde die Position auf 156,236µm korrigiert. Die Linearität des Sensorsystems wurde auf folgende Weise bestimmt: Der Piezoaktor wurde mit einem Sinussignal über den gesamten Verfahrbereich angesteuert. Die Bewegung des Aktors wurde mit dem integrierten Sensor und dem Laserstrahl Interferometer ermittelt.
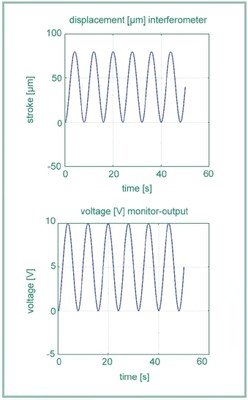
Abb. 9.2.1. sensor output signal and signal from laser beam interferometer
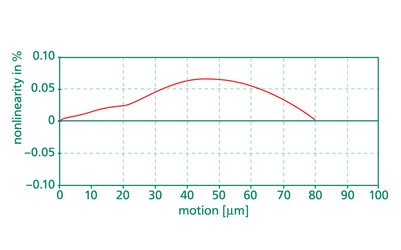
Abb. 9.2.2. linearity of a PX100 with strain gauge
9.3. Wiederholgenauigkeit (Reproduzierbarkeit) – ISO 5725
Die Wiederholgenauigkeit bezeichnet den Fehler, der entsteht, wenn die gleiche Position aus der gleichen Richtung immer wieder von Neuem angefahren wird. Zur Erreichen einer bestimmten Position muss immer die gleiche Modulationsspannung angelegt werden. Der Unterschied zwischen Modulationsspannung und Monitorsignal wird durch die Steuerung auf null gesetzt. Die Abweichung der erreichten unterschiedlichen Positionen wird durch den Wert der Wiederholgenauigkeit angegeben. In dem mitgelieferten Kalibrier-Protokoll wird der absolute und relative Wert der Wiederholbarkeit angegeben.
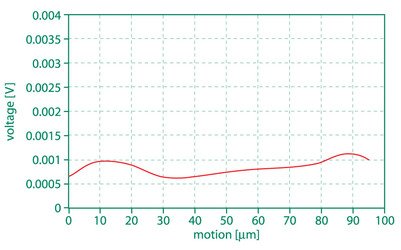
Abb. 9.3.1. typ. Wiederholgenauigkeit für einen PX100 mit kapazitivem Messsystem
Beachten Sie:
Die genaue Position der Piezoelemente kann am Piezoverstärker aufgrund der Displayeigenschaften (z.B. Trägheit) der nicht immer exakt abgebildet werden. Für hochgenaue Positionierungsaufgaben ist es empfehlenswert, die Position über den Monitorausgang zu überwachen. Dazu ist ein entsprechendes digitales Voltmeter notwendig.
9.4. Dynamische Eigenschaften eines Closed Loop Systems
Wie erwähnt, beeinflussen alle Einzelteile eines closed loop-Systems die dynamischen Eigenschaften. Dies schließt die Eigenschaften des Aktors, des Sensors und der Elektronik mit ein.
Bitte beachten Sie:
Wenn man von den Eigenschaften des Aktors spricht, bedeutet dies, der Aktor ist in das reale Experiment integriert. Zusatzmassen oder weitere Kräfte von außen können die dynamischen Eigenschaften drastisch beeinflussen. Da wir nicht wissen, wie unsere Aktoren im Einzelfall eingesetzt werden, haben wir die Aktoren in unseren Experimenten nicht mit zusätzlichen Massen beladen. Sie finden weitere Details über die dynamischen Eigenschaften von Aktoren auch im Kapitel 5.
Die Regelelektronik, unter Verwendung der Regelalgorithmen (P, PI, PID etc.) beeinflusst auch das dynamische Verhalten. Jedes Steuersystem muss mit dem dazugehörigen Aktor kalibriert werden. Ändern Sie keine Elemente, Verstärkerkomponenten oder Aktoren eines Regelsystems!
Um genaue Ergebnisse der dynamischen Eigenschaften zu erhalten, müssen die Dämpfungskurve und die Phasenverschiebung über die Frequenzänderung gemessen werden. Die dynamische Funktion zum Betreiben des Elementes sollte mit Vorsicht auf die beeinflussende Frequenz untersucht werden.
Die Ansteuerfrequenz muss kleiner sein als die maximale Frequenz (Resonanzfrequenz) des gesamten Systems. Um dies zu gewährleisten, sollte jede Kurve, die sich von einer Sinuswellenfunktion abweicht analysiert werden. Nur so kann sichergestellt werden, dass keine unerwünschten Anregungsfrequenzen erzeugt wird, welche die maximale Frequenz übersteigt. Daher muss eine Fourier-Transformation vorgenommen werden.
Eine Näherung in der Regelungstheorie besagt, dass die maximale Systemfrequenz eines rückgekoppelten Systems zehnmal kleiner sein sollte als die niedrigste Eigenfrequenz des Regelungssystems.
Um einen Eindruck davon zu geben, was in einem geschlossenen Regelkreis erreicht werden kann, haben wir Untersuchungen mit den Elementen PX100 – ausgerüstet mit einem DMS-Sensor – durchgeführt.
Das Element wurde mit einer Rechteck- Funktion von 10Hz mit einer Amplitude von etwa 50% des vollen Hubbereichs angesteuert. Wir bestimmten die Anstiegszeit, in der das geregelte System eine Genauigkeit von 99% und 99,9% der endgültigen Position erreichte. (siehe Abb. 9.4.1)
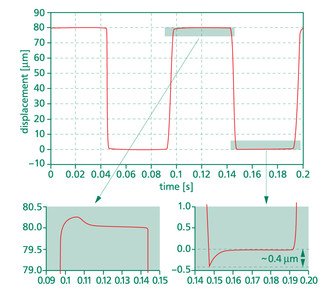
Abb. 9.4.1. Anstiegszeit eines closed loop-Systems PX100 mit einem DMS-Messsystem
9.5. Kalibrier-Protokoll für Closed Loop Systeme
Jedes closed loop-System wird, wenn nicht anders vereinbart, kalibriert. Nur so können die exakten Werte für die Linearität und die Reproduzierbarkeit erreicht werde.
Diese Informationen finden Sie immer im mitgelieferten Kalibrier-Protokoll des Systems zusammengefasst.
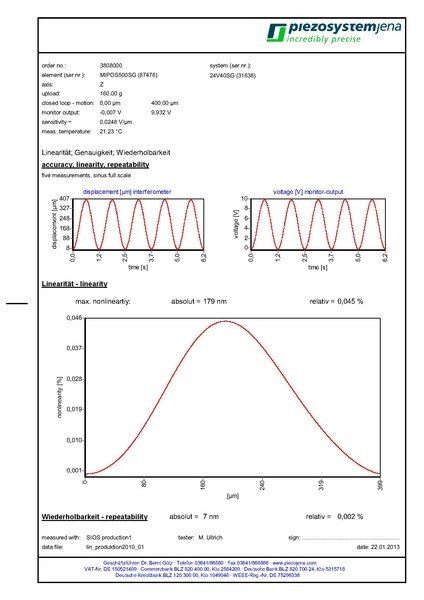
Bedeutung der Parameter:
a) gesamter Verfahrbereich (auf diesen Weg wurde kalibriert)
b) 1. Spannungssignal am Monitorausgang (entspricht kalibrierter Position)
c) 2. Spannungssignal am Monitorausgang (entspricht kalibrierter Position)
d) Wert der Empfindlichkeit des Systems (siehe auch 9.2.1)
e) Angabe der Nicht-Linearität Beispiel: @200µm = 0,0447% = 179nm
Berechnung der Nichtlinearität in nm anhand der Messwerte des Kalibrierprotokolls:


Nichtlinearität = 179nm
Piezoprinzip-Themen
- 1) Piezoelektrischer Effekt
- 2) Bauformen
- 3) Eigenschaften und Leistung
- 4) Statisches Verhalten
- 5) Dynamisches Verhalten
- 6) Systeme mit integrierter Wegübersetzung
- 7) Simulation dynamischer Eigenschaften
- 8) Closed Loop Systeme
- 9) Messsysteme
- 10) Elektronische Ansteuerung
- 11) Lebensdauer und Zuverlässigkeit
- 12) Verwendungsrichtlinien
- 13) Hochleistungspiezos
- 14) Piezo-Shaker
- 15) Piezo-Stoßgeneratoren






