3. Eigenschaften und Leistung
3.1 Ausdehnung
Die relative Dehnung S = l/L0 (ohne Betrachtung äußerer Kräfte) eines Piezoaktors ist proportional der angelegten Feldstärke und beträgt typ. 0,1 – 0,13 % (für eine Feldstärke von E=2kV/mm).
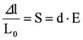
S – relative Dehnung (ohne Dimension)
d = dii – Materialparameter
E = U/ds piezoelektrische Ladungskonstante – äußere elektrische Feldstärke
U – angelegte Spannung
ds – Dicke einer einzelnen Piezoscheibe
Damit erhöht sich mit der angelegten Spannung auch die erreichbare Ausdehnung. Der Zusammenhang ist nicht genau linear, wie nach Gleichung (3.1), die Kennlinie wird mit der Hysteresekurve beschrieben. Maximale Ausdehnungen, die technisch beherrschbar sind (ohne Hebelübersetzung) betragen bis 300 µm – bei einer Baulänge von ca. 300 mm!
Typische Aktoren bewegen sich im Hubbereich 20 µm bis 100 µm (Baulänge bis 100 mm). Für größere Bewegungen werden hebelübersetzte Systeme eingesetzt.
Eine weitere Alternative zum Erreichen größerer Wege ist die Kombination von piezoelektrischen und mechanischen bzw. elektromotorischen Systemen. Mit diesen Kombinationen lassen sich Bewegungen im cm Bereich erreichen. Die Spielfreiheit der Bewegung über den gesamten Bereich ist dann aber nicht mehr gegeben.
3.2 Hysterese
Aufgrund ihrer ferroelektrischen Eigenschaften haben PZT Keramiken ein typisches Hystereseverhalten. Bei Anlegen einer bipolaren Spannung zeigt ein Piezoelement folgende Kennlinie:
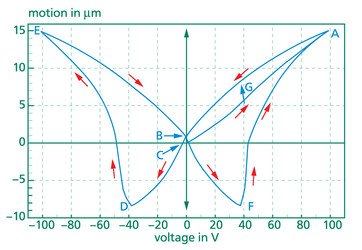
Das Piezoelement dehnt sich bei Anlegen einer positiven Spannung aus. Neben der Begrenzung der maximalen Ausgangsspannung (Punkt A) durch die Durchschlagsfestigkeit des Materials zeigt der Piezoeffekt gewisse Sättigungseffekte. Nach Entfernen der Spannung bleibt eine remanente Polarisierung (Punkt B). Diese remanente Polarisierung kann durch Ansteuerung mit einem negativem Feld (Koerzzitivfeldstärke; Punkt C) aufgehoben werden. Bei weiterer Erhöhung der negativen Spannung zeigt der Piezoaktor eine Kontraktion, es beginnt eine Umpolarisierung der Keramik. Im Punkt D ist die Umpolarisierung für die Mehrzahl der Dipole erfolgt. Bei weiterer Erhöhung der negativen Spannung erfolgt nun wieder eine Ausdehnung des Materials bis zur maximalen Ausdehnung (Punkt E).
Die Wegnahme der Spannung führt wiederum zu dem Punkt B entsprechend der remanenten Polarisierung. Bei Erhöhung der Spannung kann nun wieder eine Kontraktion bis zur Umpolarisierung (Punkt F) beobachtet werden. In dieser Betriebsart wird ein Piezoaktor im Regelfall nicht betrieben.
Die Schmetterlingskurve zeigt, dass durch das Anlegen der bipolaren Spannung die Position des Piezoelementes nicht genau bestimmt werden kann. Z.B. kann bei der gleichen Spannung das Element in Position G oder F sein.
So arbeitet man in der Regel mit der unipolaren Spannung außerhalb des Bereichs der Sättigung, des Abbaus und außerhalb des Bereichs der Polarisationsänderungen. Die Piezoelemente zeigen die bekannten Aufweitungseigenschaften.
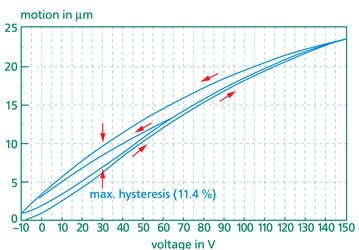
Um größere Bewegungen zu erzielen, ist es möglich mit negativen Spannungen der Größenordnung von 10V bis 20V zu arbeiten (für Mehrschichtsysteme). Deswegen sind unsere Elemente auf einen Spannungsbereich von -20V bis +130V abgestimmt.
Bei Anlegen einer unipolaren Spannung erhöht man die typische Hysterese-Kennlinie piezoelektrischer Bauelemente. Diese Hysterese beträgt 10 – 15 % des maximalen Hubes und ist in der ferroelektrischen natur der Piezokeramik begründet. Für viele Anwendungsfälle wirkt sich die Eigenschaft der Hysterese nicht störend aus. In einem kleinen Spannungsbereich fällt die Hysterese kleiner aus. (Bild 3.2.2)
Jedes Piezoelement von piezosystem jena wird mit der gemessenen Hysteresekurve ausgeliefert.
In „closed loop“ Systemen vergleicht die „closed loop“ Elektronik eine vorgegebene oder gewünschte Position (z. B. den Modulationseingangssignal) mit der vom Sensorsystem augenblicklich gemessenen Position. Alle Abweichung von beiden Signalen wird korrigiert. Durch ihre Genauigkeit zeigen „closed loop“ Systeme keine Hysterese. Für weitere Informationen siehe Kapitel 8 und 9.
Da die Lebensdauer piezoelektrischer Aktoren im Wesentlichen mit von der Betriebsspannung beeinflusst wird, empfehlen wir für den permanenten Industrieeinsatz Steuerspannungen bis 100V. Dies gilt besonders für Applikationen bei denen der Aktor seine maximale Expansion statisch halten muss. Bitte beachten Sie hierzu auch Kapitel 11 – Lebensdauer
3.3. Auflösung
Unabhängig von der Hysterese zeigt der Piezoeffekt als Festkörpereffekt eine sehr hohe Auflösung. So wurde der Piezotisch PX 38 von piezosystem jena (max. Hub in x-Richtung: 38 µm) in einer Interferometeranordnung getestet und Wegänderungen von 1/100 nm realisiert und nachgewiesen. Die Auflösung von Piezoelementen wird durch das Rauschverhalten und die Restwelligkeit des elektrischen Steuersignals bestimmt. Dieses wurde durch piezosystem jena bei der Entwicklung der Spannungsverstärker entsprechend berücksichtigt (siehe auch Kapitel 9.1 und 10.1).
Beispiel 6
Die Piezosteuereinheit NV 120/1 hat ein Spannungsrauschen von < 0,3 mV. Bezogen zur Gesamtspannung von 150 V bedeutet dieses einen Restwelligkeit 2*10-5. Damit werden bei einem Piezoelement mit einem Gesamthub von z.B. 20 µm die durch die Restwelligkeit des Signals hervorgerufenen Schwankungen auf ca. 0,04 nm begrenzt.
Auch bei Spannungsverstärkern beraten wir Sie gern über optimale Lösungen!
piezosystem jena bietet ein komplettes Programm von Spannungsverstärkern an. Applikationsgerecht kann zwischen kompakten Geräten, modularen Verstärkern im 19″ Rack-Einschubsystem und natürlich einer Vielzahl an OEM Ausführungen gewählt werden.
3.4 Polarität
Piezoelemente von piezosystem jena sind grundsätzlich für positive Versorgungsspannungen ausgelegt Bei Anlegen einer invertierten Spannung von bis maximal 10 % der Gesamtspannung (z.B. -10 V für 130-V-Mehrschichtelemente) kontrahiert der Aktor und leistet auf diese Weise einen größeren Gesamthub. Vermeiden Sie höhere negative Spannungen bei Piezoelementen mit positiver Polarität, da sonst Umpolarisationseffekte auftreten können!
3.5 Steifigkeit
Die Steifigkeit ist eine sehr wichtige Größe zur Bestimmung verschiedener Eigenschaften wie Resonanzfrequenz und Blockierkraft. Ein Piezotranslator kann in erster Näherung als mechanisches Element mit einer Federsteifigkeit betrachtet werden.
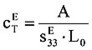
Die Steifigkeit ist proportional zum Aktorquerschnitt A und nimmt mit zunehmender Baulänge L0 ab. Die Abhängigkeit ist aber noch komplexer. Die Steifigkeit wird auch von anderen Parametern beeinflusst. So wirkt sich die elektrische Beschaltung des Aktors auf seine Steifigkeit aus. Seine maximale Steifigkeit zeigt ein Aktor bei offenen Elektroden.
Wenn keine Verbindung der Elektroden untereinander besteht, kann die Energie nicht abgeführt werden, weshalb sich die Steifigkeit maximiert.
Hinweis:
Bitte beachten Sie, dass die unter 3.5.1 gegebene Formel nur eine Näherung zur Berechung der Steifigkeit darstellen kann. Faktoren wie die Betriebsart (statisch, dynamisch) beeinflussen die Steifigkeit ebenso wie die zu bewegende Last, elektrische Einflüsse die aus der Signalart resultieren (Groß- und Kleinsignalverhalten) So kann sich die unter Kleinsignalverhalten gemessene Kapazität eines Aktors bei Vollhub und dem daraus resultierenden Großsignalverhalten nahezu verdoppeln! Weiterhin lassen sich mit der Formel 3.5.1 die erwarteten Eigenschaften der Piezoelemente nur grob berechnen.
Beispiel 7:
Ein Aktor mit den Dimensionen von 5 x 5 x 9 mm³ hat eine Steifigkeit cT1E = 120N/µm. Bei gleichem Aufbau (Querschnitt; Material und Zusammensetzung) aber doppelter Länge von 18 mm halbiert sich die Steifigkeit entsprechend Gl. 3.5.1. cT2E = 60 N/µm. Wird wiederum ein Aktor mit gleichem Aufbau aber 4fachen Querschnitt verwendet (Maße 10 x 10 x 18 mm³), so weist dieser Aktor auch die vierfache Steifigkeit auf cT3E = 240 N/µm.
3.6. Temperaturverhalten
Zum Erreichen höchster Positioniergenauigkeiten ist die Kenntnis der Temperaturverhältnisse am Messaufbau und des Temperaturverhaltens der verwendeten Bauelemente von großer Bedeutung. Der thermische Ausdehnungskoeffizient von Stahl beträgt 12·10-6K-1. Bei einem Würfel von 10x10x10 mm3 führt eine Temperaturänderung von 1K zu einer Ausdehnung in jeder Richtung > 0,1 µm. Deshalb ist die Kalibrierung der Piezoelemente mit integrierten Messsystemen stark von der Temperatur abhängig. Fehler und Abbrüche können auftreten, wenn die Arbeitstemperatur von der Kalibriertemperatur abweicht.
Spricht man von thermischen Einflüssen, muss man prinzipiell drei Effekte beachten
a) Das Temperaturverhalten von Piezokeramik ist stark materialabhängig. Multilayeraktoren, wie sie von piezosystem jena eingesetzt werden, zeigen einen negativen Temperaturverlauf αNV = -5·10-6-1 bei Temperaturen bis 120 °C. Hochvoltkeramiken, die ebenfalls von piezosystem jena eingesetzt werden, weisen hingegen einen positiven Temperaturkoeffizienten αHV= (7-10) ·10-6-1
Mehrschichtige Stapelaktoren zeigen einen negativen Temperaturkoeffizienten von αNV ≈ -6-10-6 K-1 im Bereich bis 120°C.
Die thermische Längenänderung eines gesamten Kurzschlussaktors (z. B. der Serien P, PA, PAHL) ist die Summe der thermischen Ausdehnungen der Piezokeramik und der Metallteile des Aktors.
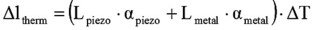
Δltherm = thermische Ausdehnung des Aktors
Lpiezo = Länge des Piezostapels
Lmetal = Länge des Metallkäfigs
αpiezo = Temperaturkoeffizient Piezokeramik
αmetal = Temperaturkoeffizient des Metallkäfigs
ΔT = Temperaturdifferential
Beispiel 8:
Ändert sich die Umgebungstemperatur um einen Aktor des Types PA 16/12 von 20°C auf 30°C, so resultiert daraus eine Längenänderung bei einer angelegten Spannung von 130V (max. Hub) von:
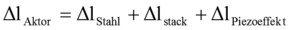
Der Gehäuse aus Edelstahl hat eine Länge von 16mm:
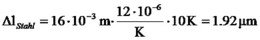
Die Piezokeramik hat eine Länge von 19mm:
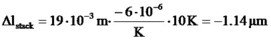
Die Differenz ist Δlaktor=0.78µm
b) Der Einfluss der Temperatur auf den Piezoeffekt kann im Bereich der Raumtemperatur vernachlässigt werden. Im Bereich tiefer Temperaturen (< 260K) nimmt der Piezoeffekt mit ca. 0,4%/K ab.

Im Bereich tiefer Temperaturen, wie z.B. für flüssiges Nitrogen (T1 ca. 77 K) kann mit 20 – 30 % des Hubes bei Raumtemperatur (T0) gerechnet werden.Unter der Annahme, dass die Beziehung zwischen der Veränderung der piezoelektrischen Expansion und der Temperatur linear verläuft, kann die Temperatur berechnet werden:
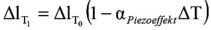
ΔlT1= Ausdehnung bei T1
ΔlT0= Ausdehnung bei Zimmertemperatur
ΔT=T0-T1
αpiezoeffekt =Temperaturkoeffizient des Piezoeffekts
Im Bereich von 260K bis 390K kann die Veränderung des Piezoeffekts vernachlässigt werden.
Beispiel 9:
Zur Abschätzung welcher Hub bei einem PX 100 (Nennhub 100µm) bei -195°C (Flüssiger Stickstoff) im Vergleich zu einer Temperatur von -10°C noch zur Verfügung steht, errechnet man zuerst die Temperaturdifferenz. Diese ergibt sich mit ΔT =185K. Nach obiger Kalkulation ist dann ein Resthub von ca. 25µm zu erwarten.
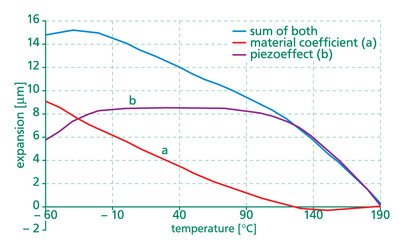
Figure 3.6.1. Temperaturabhängigkeit der Piezokeramik LPiezo = 18mm (für Multilayeraktoren PA 16/12) bei Raumtemperatur
c) Eine Veränderung der ferroelektrischen Hysterese ist ebenfalls bei tiefen Temperaturen zu beobachten. Durch eine Veränderung der ferroelektrischen Polarisation erfolgt eine deutliche Abnahme der Hystereseerscheinung. Bei einer Temperatur von 4K tritt keine wesentliche Dipoländerung mehr auf. Und daher ist der Effekt der Hysterese zu vernachlässigen. Bei Raumtemperatur kann der Einfluss dieser Temperaturschwankungen auf die Hysterese ebenfalls vernachlässigt werden.
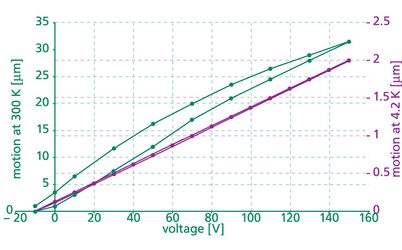
Abb 3.6.2. Hysteresekurve eines PA25 Elementes bei Raumtemperatur und bei 4K
Zu berücksichtigen:
Obwohl der Piezoeffekt mit sinkender Temperatur abnimmt, können piezoelektrische Aktoren prinzipiell bei sehr niedrigen Temperaturen arbeiten – bis zur Temperatur von flüssigem He (4K).
Wenn Sie in einem Tieftemperaturbereich arbeiten wollen, teilen Sie uns dies bitte mit, damit wir den Aktor für diesen Temperaturbereich vorbereiten können.
Piezotische
Das Temperaturverhalten für Elemente in einem Festkörpergelenksystem hängt sowohl vom Temperatur-Effekt für das Piezoelement als auch vom Verhalten des Gelenksystems ab. Es kann von dem oben beschriebenen Verhalten für den reinen Piezoaktor abweichen. Auf Grund der unterschiedlichen Konstruktionen für verschiedene Komponenten kann keine allgemeingültige Gesetzmäßigkeit abgeleitet werden.
Piezotische in einer „closed loop“ Anwendung
Bitte achten Sie im Betrieb auf die Einhaltung der Temperatur, die der Temperatur bei der Kalibrierung entsprechen sollte. Diese Information ist auf jeden Kalibrierprotokoll von piezosystem jena vermerkt. Nur bei dieser Temperatur erreichen Piezoelemente die höchste Genauigkeit.
3.7 Kapazität
Ein gestapelter Aktor besteht aus Keramikscheiben als Dielektrikum und angrenzenden Elektroden. Damit stellt er eine Parallelschaltung von Kapazitäten dar, die sich somit addieren.
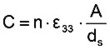
n – Anzahl der Einzelscheiben
ε33 – Dielektrizitätskonstante
A – Scheiben – bzw. Stapelquerschnitt
ds – Dicke einer Einzelscheibe
Beispiel 10:
Ein Niedervoltstapel mit einer (aktiven) Länge von 16mm, einer Querschnittsfläche von 25 mm2 und einer Scheibendicke von 110 µm besteht aus ca. 144 Keramikschichten. Mit der relativen Dielektrizitätskonstanten von εr = 5400 erhält man eine Aktorkapazität von ca. 1,6 µF.
Kapazität Niedervoltstapel – Kapazität Hochvoltstapel
Betrachten wir folgenden Vergleich:
Beispiel 11:
Ein Niedervoltstapel (Index 1; Parameter wie Beispiel 10) wird ersetzt durch ein Hochvoltelement gleicher aktiver Länge (Index 2). Der Einfachheit halber werden gleiche Dielektrizitätskonstanten beider Stapel angenommen, zur Anwendung kommt Gleichung (3.7.1.). Die Scheibendicke des Hochvoltstapels ist um den Faktor 5 höher (ds2 = 5·ds1), dementsprechend ist die Scheibenanzahl um den Faktor 5 niedriger (n2 = 1/5·n1). Damit ergibt sich für die Kapazität des Hochvoltstapels C2 = C1/25.
Bei Ersatz eines Hochvoltstapels durch einen Niedervoltstapel wird eine kleinere Ansteuerspannung benötigt. Dafür steigt die Kapazität des Aktors quadratisch an.
Beachten Sie bitte:
Aufgrund ihrer höheren Kapazität benötigen Niedervoltaktoren wesentlich höhere Lade- und Entladeströme. Dieser Sachverhalt spielt bei statischen und quasistatischen Anwendungen eine untergeordnete Rolle, wird aber bedeutend für dynamische Anwendungen.
Achtung!
Die piezoelektrischen Eigenschaften von Aktoren sind nicht konstant, wie es in einigen einfachen Beschreibungen erklärt wird. In Datenblättern und in der Literatur angegebene Parameter von Piezoaktoren beziehen sich vorwiegend auf das Kleinsignalverhalten und sind feldstärkeabhängig. Beim Großsignalbetrieb ergeben sich Abweichungen. So zum Beispiel ist die Großfeldkapazität ca. doppelt so hoch wie oben angegebene Kleinsignalwerte.
3.8. Drift/Kriechen (Open Loop Systeme)
Eine weitere charakteristische Eigenschaft von Piezoelementen ist eine leichte Driftbewegung nach Einstellen einer bestimmten Spannung. Dieses Nachlaufen ist durch Nachpolarisation der Keramik begründet. Ein Sprung in der angelegten Spannung sorgt für eine Anfangsbewegung, die sich über eine längere Zeit nur noch geringfügig ändert. Die anschließende Driftbewegung befindet sich in einer Größenordnung von 1% – 2% und hängt von der Ausdehnung l, vom keramischen Material (Parameter ?), den externen Strömen und von der Zeit ab. Die Abhängigkeit von der Zeit kann logarithmisch dargestellt werden; die Drift nimmt nach einigen Sekunden nach Einstellen einer Spannung schnell ab.
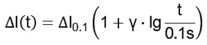
Δl0,1 – Ausdehnung 0,1s nach Beendigung des Stellvorgangs
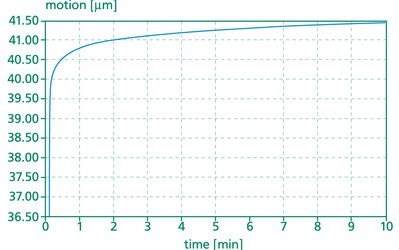
Abb. 3.8.1. Drift eines PU 40
In diesem Fall erzielen wir einen Wert für γ≈ 0.015. Der Wert für γ hängt von mehreren Größen ab: dem Material, der Konstruktion und den Umgebungsbedingungen (z.B. Kräfte ab).
Wenn die Bewegung gestoppt wird, wird die Drift nach ein paar Sekunden gestoppt.
Wiederholbarkeit
Bei periodischer Ansteuerung mit einem festen wiederkehrenden Zeitregime spielt die Drift eine untergeordnete Rolle. Auf Grund der kurzen Zeitintervalle ist sie sehr klein. Außerdem geht sie bei jeder Wiederholung der Bewegung gleichermaßen ein. Diese wurde an folgendem Experiment bestätigt. (Bild 3.8.2.) Eine Spiegelhalterung von piezosystem jena wurde mit einem normalen Spannungsverstärker über einen Funktionsgenerator mit einer Sinusschwingung angesteuert. Der gesamte Schwingungsbereich betrug ca. 380″, im Bild ist ein Ausschnitt 10″ (Bereich: -302″ bis -312″) dargestellt. Es konnte gezeigt werden, dass die Wiederholungsgenauigkeit <0,1″ beträgt – ohne den Aufwand eines Messsystems und Regelkreises.
Damit wird eine sehr gute Reproduzierbarkeit von periodischen Vorgängen erreicht, die hauptsächlich durch die Parameter der Elektronik (z.B. Funktionsgenerator und Spannungsverstärker) bestimmt werden.

Abb. 3.8.2. Reproduzierbarkeit einer Kippbewegung bei periodischer Ansteuerung
3.9 Vakuumbetrieb
Piezoelemente arbeiten prinzipiell auch im Vakuum. Das Problem, welches sich dabei stellt, ist das Ausgasverhalten der Piezoaktoren. Um die Piezoaktoren vor Zerstörung durch Überschläge zu schützen und auch die Umgebung vor hoher Spannung zu schützen, werden Piezoaktoren von piezosystem jena mit einer Isolationsschicht versehen und teilweise zusätzlich vergossen. Diese Isolationsmaßnahmen verschlechtern natürlich das Ausgasverhalten von Piezoaktoren.
Aus diesem Grund werden Piezoaktoren für den Vakuumeinsatz besonders behandelt und weitgehend ohne Isolationsmaterialien versehen. Zudem kommen in der Fertigung dieser Piezoaktoren nur vakuumtaugliche, besonders ausgasarmen Materialien (z. B. Spezialklebstoffe) zum Einsatz. Mit diesen Maßnahmen wird ein hervorragendes Ausgasverhalten erreicht, welches eine Integration auch in UHV Systeme ermöglicht.
Achtung!
Im Druckbereich zwischen 100hPa bis 0,1hPa besitzen üblicherweise verwendete Gase einen niedrigen Isolationswiderstand. Durch die z.T. fehlenden Isolationsmaßnahmen an den Piezoelementen für den Vakuumbetrieb dürfen diese im o. g. Druckbereich nicht betrieben werden! Spannungsüberschläge können anderenfalls zur Zerstörung der Elemente führen, gegebenenfalls auch zu Beschädigungen der Vakuumanlagen!
Beispiel 12:
Ein Piezo- Spaltantrieb der Serie PZS 1 wurde speziell für Vakuumbetrieb ausgelegt. Die Untersuchung zeigte, bis zu einem Druck von 5·10-9hPa wirkte sich das Ausgasverhalten der Komponenten des Spaltantriebes nicht störend aus. Überhitzung, Ausbacken der Piezoelemente für Vakuumapplikationen Piezoaktoren von piezosystem jena können problemlos bis 80°C erwärmt werden und auch bis zu diesem Bereich arbeiten. Speziell vorbereitete Elemente dürfen bis 150°C ausgeheizt werden (siehe auch Kapitel 3.10). Nach dem Abkühlen sollte die Steuerspannung langsam erhöht werden, um eine erneute Repolarisation durchzuführen.
3.10 Curie-Temperatur
Wird Piezokeramik bis zur materialabhängigen Curietemperatur Tc erwärmt, so geht die Ausrichtung der Dipole vollständig verloren. Das Keramikmaterial geht vom ferroelektrischen Zustand in den paraelektrischen Zustand über. Ein piezoelektrischer Effekt ist jetzt nicht mehr vorhanden.
Die Curietemperatur ist materialabhängig. Multilayeraktoren von piezosystem jena weisen eine Curietemperatur von typ. 150°C. Typische Werte für Hochvoltaktoren liegen bei 250°C.
Werden Piezoaktoren bis in die Nähe der Curietemperatur erwärmt, so beginnt thermische Depolarisation einzusetzen. Aus diesem Grund sollten Piezoaktoren deutlich unterhalb (bis etwa Tc/2- gewöhnlich bis 80°C) ihrer Curietemperatur betrieben werden.
Eine thermisch depolarisierte Piezokeramik kann bei hohen Feldstärken erneut polarisiert werden. Daher lässt sich die Piezokeramik auch in UHV-Anlagen mit Ausheizung verwenden.
Die Temperaturbelastung von Piezoaktoren (Eigenerwärmung) kann bei statischer und quasistatischer Betriebsweise vernachlässigt werden. Relevant wird sie bei dynamischer Ansteuerung und sollte in diesen Fällen unbedingt beachtet werden (siehe auch Kapitel 5: dynamisches Verhalten).
Piezoprinzip-Themen
- 1) Piezoelektrischer Effekt
- 2) Bauformen
- 3) Eigenschaften und Leistung
- 4) Statisches Verhalten
- 5) Dynamisches Verhalten
- 6) Systeme mit integrierter Wegübersetzung
- 7) Simulation dynamischer Eigenschaften
- 8) Closed Loop Systeme
- 9) Messsysteme
- 10) Elektronische Ansteuerung
- 11) Lebensdauer und Zuverlässigkeit
- 12) Verwendungsrichtlinien
- 13) Hochleistungspiezos
- 14) Piezo-Shaker
- 15) Piezo-Stoßgeneratoren






